Nous ne savons pas…
Nous ne savons pas combien d'Univers il y a en dehors de notre Univers observable.
L'Univers observable semble avoir une géométrie "plate" ( au sens 3D, pas en 2D). S'il est vraiment globalement plat, cela continue indéfiniment, c'est-à-dire qu'il y a une masse infinie. Cependant, tout comme la Terre semble plate à petites échelles, il se pourrait très bien que l'Univers ait une autre géométrie à des échelles plus grandes que celles que nous pouvons observer.
Un article récent ( Di Valentino et al. 2019) a revendiqué des preuves d'une géométrie "positivement courbée", ce qui implique que l'Univers n'est que (très grossièrement et avec des incertitudes élevées) trois fois plus grand que ce que nous voyons (voir cette réponse et les commentaires pour le calcul). Cependant, les auteurs en ont sélectionné un parmi plusieurs ensembles de données de Planck Collaboration (2018), et les preuves ne sont pas convaincantes.
… et nous ne le faisons pas. attention
Cependant, peu importe si l'Univers est fini ou infini, nous ne prenons en compte la masse en dehors de l'Univers observable dans aucun calcul. Cette masse ne nous affecte en aucun cas. La gravité voyage à la vitesse de la lumière et n'a donc pas encore eu le temps de nous atteindre. Plus important encore, en raison de la loi carrée inverse, la gravité sur tout objet est de loin dominée par les sources proches.
Eh bien, nous nous en soucions un peu
Il y a un sens dans lequel vous peut dire que la gravité est prise en compte, cependant: Les soi-disant «simulations cosmologiques» visent à simuler la formation et l'évolution de la structure à grande échelle et des galaxies de tout l'Univers. Bien sûr, nous ne pouvons pas simuler l'Univers entier, donc à la place nous en simulons une grande partie; suffisamment grand pour qu'un autre morceau de taille similaire ne soit pas statistiquement différent de celui-ci (de préférence plusieurs centaines de millions d'années-lumière de chaque côté).
Une galaxie proche du bord de la boîte de calcul, disons son côté gauche, ne ressent pas seulement la gravité des galaxies sur la droite. Cela ferait «imploser» l'univers simulé. Nous utilisons plutôt une astuce de calcul appelée "conditions aux limites périodiques", ce qui signifie qu'une particule qui passe par le côté gauche de la boîte entre immédiatement par le côté droit. Et une galaxie proche du côté gauche ressent la gravité de la matière se trouvant près du côté droit.
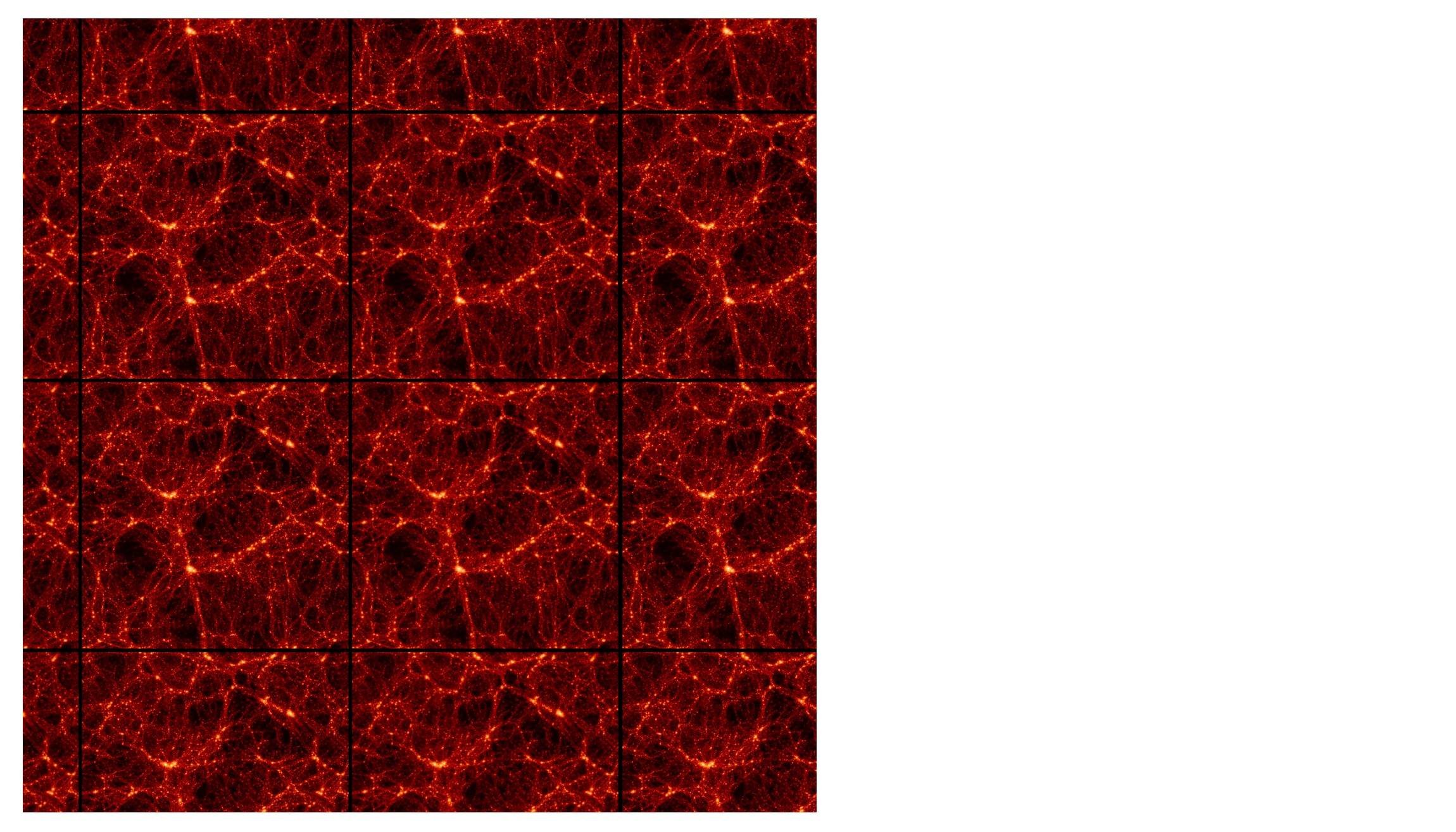
Instantané du Simulations de la Vierge ( Jenkins et al. 1998), où j'ai carrelé la boîte en plusieurs exemplaires, en insistant sur les limites périodiques.